本記事では、並進・回転・スケール変換について簡単な例をサンプルコードにて説明したのち、三つの変換を同時に実行可能な同次変換について説明します。
並進:translate
サンプルコード
import open3d as o3d # Open3Dライブラリをインポート
import copy # オブジェクトの深いコピー(deepcopy)を行うためのモジュールをインポート
from _my_module import my_function
# 全長5.0, メモリ間隔1.0, メモリ長さ0.5座標軸オブジェクトを作成
axis = my_function.create_axis(5,1,0.5)
# 原点を基準とした座標フレームを表す3Dメッシュオブジェクトを作成
mesh = o3d.geometry.TriangleMesh.create_coordinate_frame()
# 元の座標フレームをX軸方向に2.0平行移動した新しいメッシュを作成
mesh_tx = copy.deepcopy(mesh).translate((4.0, 0, 0))
# 元の座標フレームをY軸方向に4.0平行移動した新しいメッシュを作成
mesh_ty = copy.deepcopy(mesh).translate((0, 2.0, 0))
# 各メッシュの中心点(座標)を取得して表示
print(f'Center of mesh: {mesh.get_center()}') # 元のメッシュの中心点
print(f'Center of mesh tx: {mesh_tx.get_center()}') # X軸方向に移動したメッシュの中心点
print(f'Center of mesh ty: {mesh_ty.get_center()}') # Y軸方向に移動したメッシュの中心点
# すべてのメッシュを可視化
o3d.visualization.draw_geometries([axis, mesh, mesh_tx, mesh_ty])ターミナル出力結果は以下。
Center of mesh: [0.05167549 0.05167549 0.05167549]
Center of mesh tx: [4.05167549 0.05167549 0.05167549]
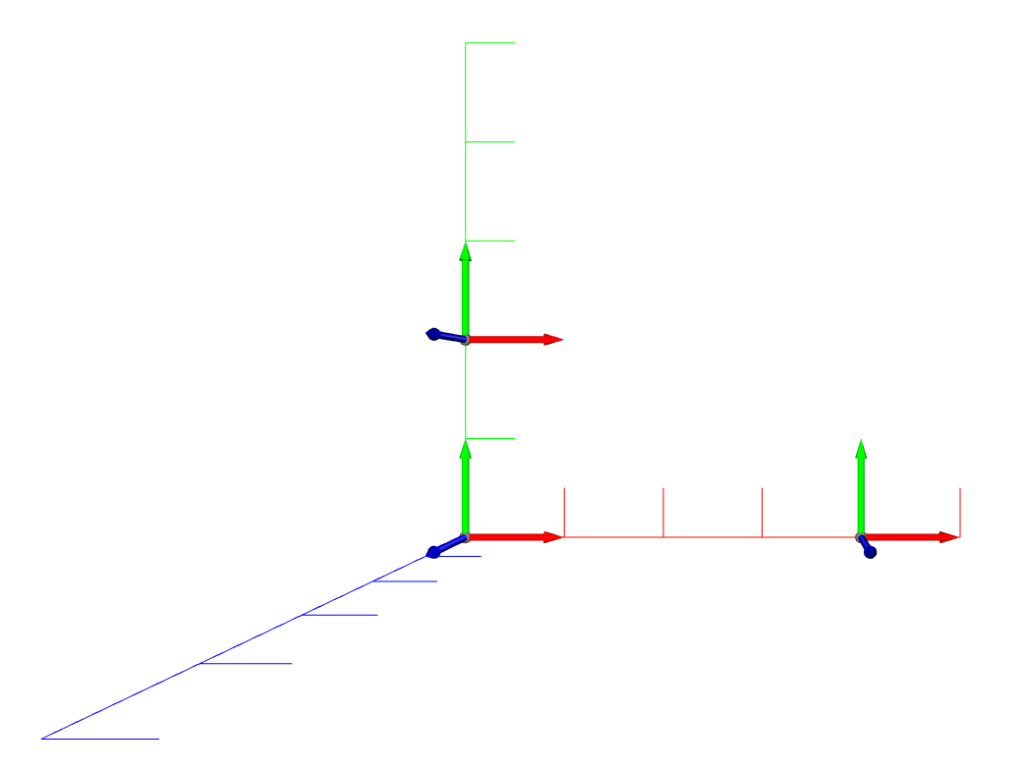
Center of mesh ty: [0.05167549 2.05167549 0.05167549]描画結果は以下。
サンプルコード解説
描画されているものは以下です。
- axis:全長5.0, メモリ間隔1.0, メモリ長さ0.5座標軸オブジェクト
- mesh:原点を基準とした座標フレームを表す3Dメッシュオブジェクト
- mesh_tx:元の座標フレームをX軸方向に2.0平行移動した新しい座標フレームメッシュ
- mesh_ty:元の座標フレームをY軸方向に4.0平行移動した新しい座標フレームメッシュ
描画結果とターミナル出力結果をみると、translata関数により、mesh_txはmeshを基準としてX方向に4、mesh_tyはmeshを基準としてY方向に2平行移動していることが確認できます。
回転:Rotation
サンプルコード
まずは、オイラー角を利用し、X軸に45度回転させる回転行列によって座標フレームを回転させてみましょう。
import open3d as o3d # Open3Dライブラリをインポート
import numpy as np # 数値計算ライブラリNumPyをインポート
import copy # オブジェクトを複製するためのモジュールをインポート
from _my_module import my_function # 自作モジュールから関数をインポート
# 全長3.0、目盛間隔1.0、目盛長0.5のカスタム座標軸を作成
axis = my_function.create_axis(3, 1, 0.5)
# 原点に単位長さの座標フレームを作成
mesh = o3d.geometry.TriangleMesh.create_coordinate_frame()
# 座標フレームをdeepcopyして複製
mesh_r = copy.deepcopy(mesh)
# X軸に45度回転させる回転行列を作成
R = mesh.get_rotation_matrix_from_xyz((np.pi / 4, 0, 0))
# 回転行列を表示(デバッグ用)
print(f'R={R}')
# 複製した座標フレームを原点を中心に回転
mesh_r.rotate(R, center=(0, 0, 0))
# カスタム軸、元の座標フレーム、回転後の座標フレームを表示
o3d.visualization.draw_geometries([axis, mesh, mesh_r])X軸(赤)を基準に、45度回転していることが見て取れる。
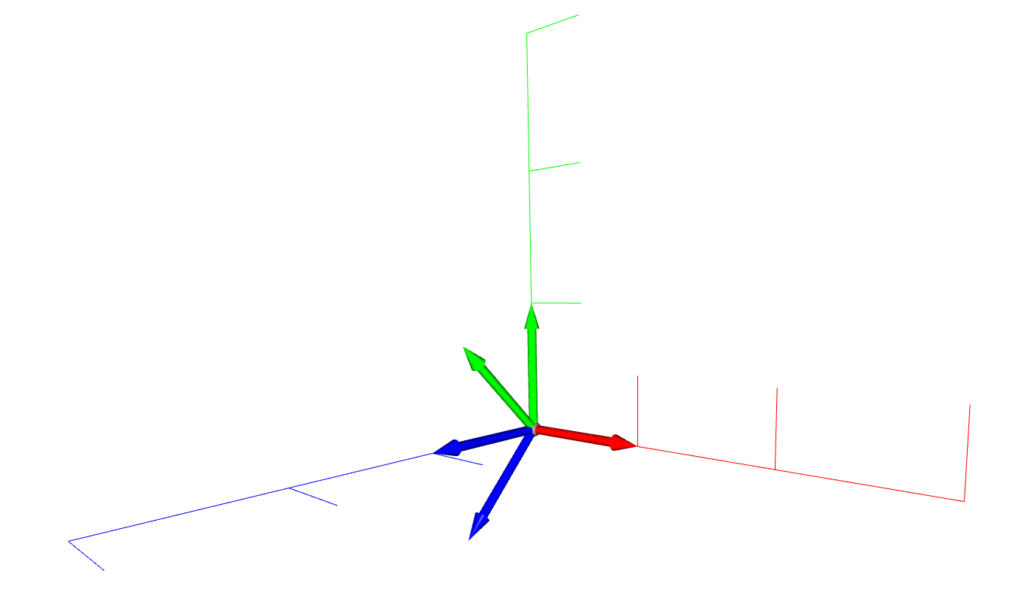
サンプルコード解説
- axis = my_function.create_axis(3, 1, 0.5)
全長3.0、目盛間隔1.0、目盛長0.5のカスタム座標軸を作成。自作モジュールを使用している。詳細はこちらの記事。 - mesh = o3d.geometry.TriangleMesh.create_coordinate_frame()
原点に単位長さの座標フレームを作成 - mesh_r = copy.deepcopy(mesh)
座標フレームをdeepcopyしてmesh_rに複製 - R = mesh.get_rotation_matrix_from_xyz((np.pi / 4, 0, 0))
X軸に45度回転させる回転行列Rを作成 - print(f’R={R}’)
回転行列を表示(デバッグ用) - mesh_r.rotate(R, center=(0, 0, 0))
複製した座標フレームを原点を中心に、回転行列Rを用いて回転する - o3d.visualization.draw_geometries([axis, mesh, mesh_r])
カスタム軸、元の座標フレーム、回転後の座標フレームを表示する
ピックアップ:回転行列を導出する関数
R = mesh.get_rotation_matrix_from_xyz((np.pi / 4, 0, 0))
上記の関数を今回取り扱うが、この関数の引数はオイラー角である。
よって、オイラー角の指定によって回転行列を戻り値として導出する。
また、関数末尾に「xyz」があるが、これは回転操作の順序をあらわしており、Open3Dでは6種類の回転操作順序を選択可能(詳細は公式リファレンスドキュメント)。
例として同じオイラー角を指定するが、回転操作順序の異なる回転行列による変換の差異を見てみよう。
- R = mesh.get_rotation_matrix_from_xyz((np.pi / 4, np.pi / 2, 0))
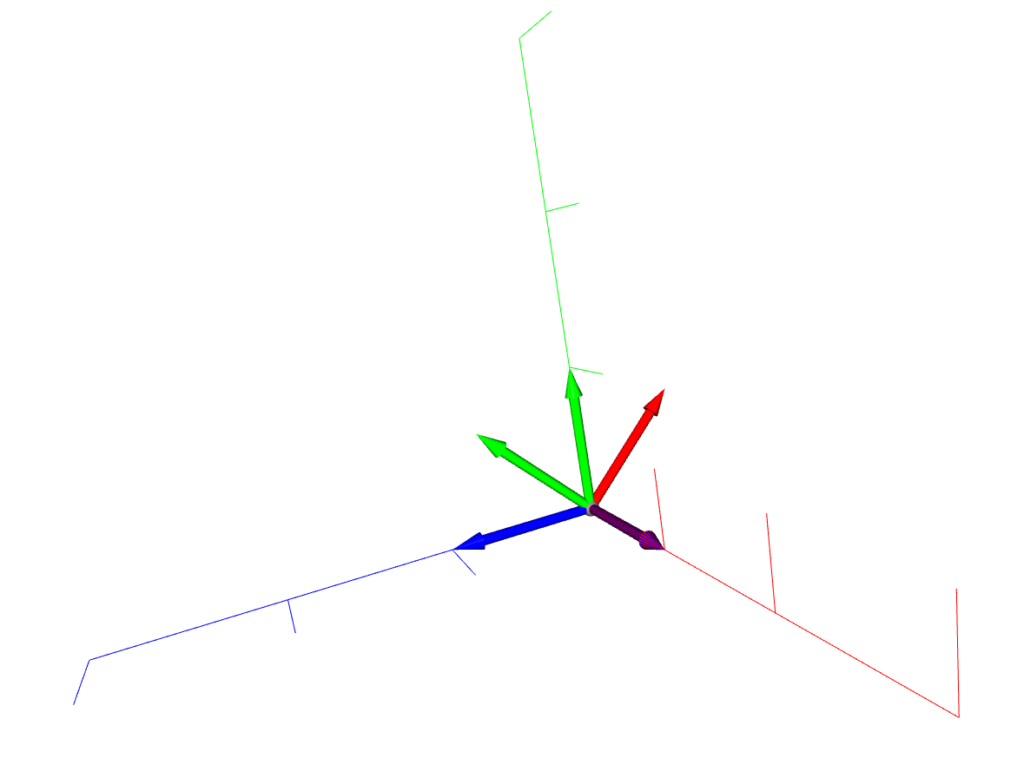
- R = mesh.get_rotation_matrix_from_yxz((np.pi / 4, np.pi / 2, 0))
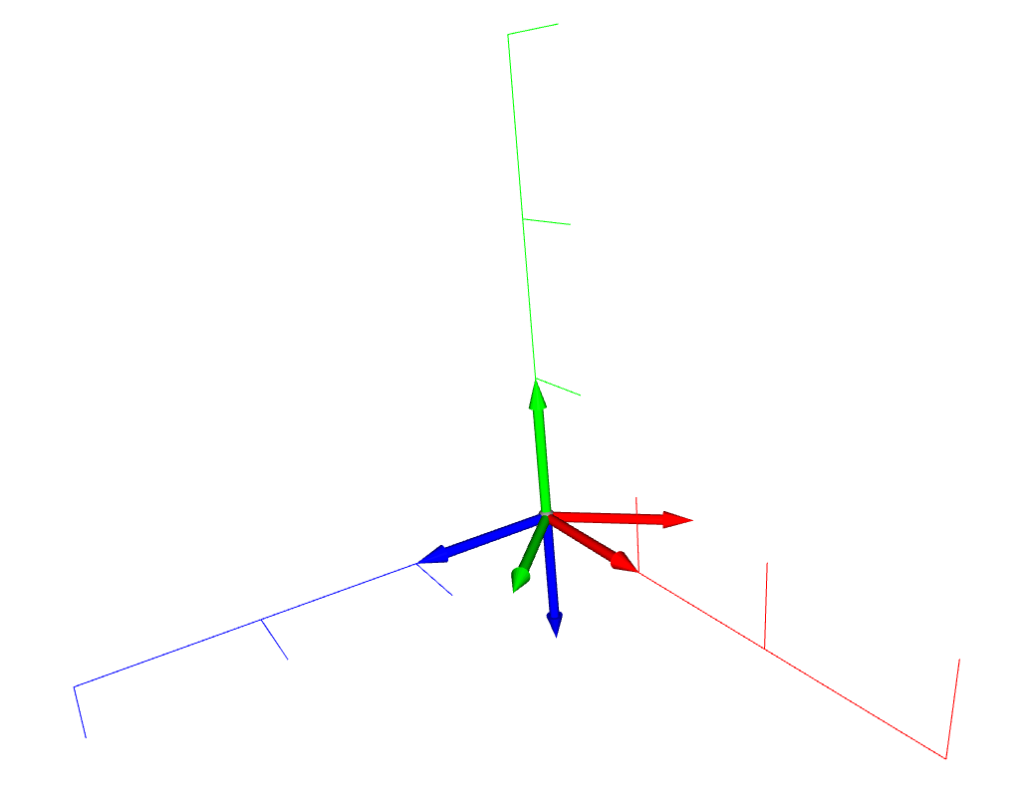
座標フレームの最終的な回転結果が異なることが確認できる。
オイラー角に関してはこちらの記事がわかりやすいです。
スケール変換:Scale
サンプルコード
座標フレームを2倍に拡大するサンプルコードを以下に示します。
import open3d as o3d # Open3Dライブラリをインポート
import numpy as np # 数値計算ライブラリNumPyをインポート
import copy # オブジェクトを複製するためのモジュールをインポート
from _my_module import my_function # 自作モジュールから関数をインポート
# 全長3.0、目盛間隔1.0、目盛長0.5のカスタム座標軸を作成
axis = my_function.create_axis(4, 1, 0.5)
# 原点に単位長さの座標フレームを作成
mesh = o3d.geometry.TriangleMesh.create_coordinate_frame()
# meshを複製してX方向に2だけ移動
mesh_s = copy.deepcopy(mesh).translate((2, 0, 0))
# 複製メッシュを中心を基準に2倍にスケーリング
mesh_s.scale(2.0, center=mesh_s.get_center())
# カスタム軸、元の座標フレーム、並進+スケール変換後の座標フレームを表示
o3d.visualization.draw_geometries([axis, mesh, mesh_s])原点からX方向に2移動させた場所に、元の座標フレームの2倍の大きさの座標フレームが表示されていることが確認できる。
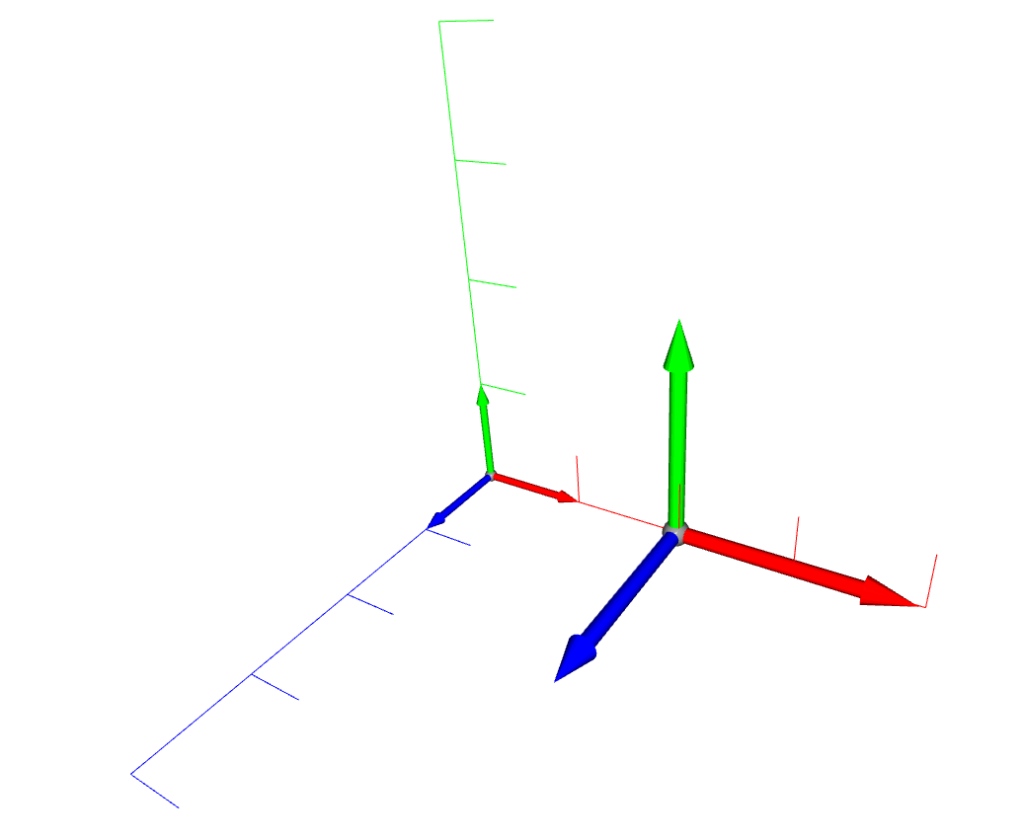
サンプルコード解説
- axis = my_function.create_axis(4, 1, 0.5)
全長4.0、目盛間隔1.0、目盛長0.5のカスタム座標軸を作成。自作モジュールを使用している。詳細はこちらの記事。 - mesh = o3d.geometry.TriangleMesh.create_coordinate_frame()
原点に単位長さの座標フレームを作成 - mesh_s = copy.deepcopy(mesh).translate((2, 0, 0))
座標フレームをdeepcopyし、かつ、tanslate関数でX方向に2移動させた座標フレームを作成 - mesh_s.scale(2.0, center=mesh_s.get_center())
複製メッシュを中心を基準に2倍にスケーリング - o3d.visualization.draw_geometries([axis, mesh, mesh_r])
カスタム軸、元の座標フレーム、回転後の座標フレームを表示する
同次変換:transform
同次変換とは?
4×4で定義され同次次変換行列を使用した変換。上述した回転・並進・スケール変換を同時に実行できる。
サンプルコード
原点に位置する座標フレームに対して、以下の変換を同次変換行列にて適用する。
- スケール変換:2倍
- 回転:Y軸中心に60度
- 並進:x方向 +1.0, y方向 +2.0
import open3d as o3d
import numpy as np
import copy
from _my_module import my_function # 自作モジュールから関数をインポート
# 全長3.0、目盛間隔1.0、目盛長0.5のカスタム座標軸を作成
axis = my_function.create_axis(4, 1, 0.5)
# 座標軸メッシュ作成
mesh = o3d.geometry.TriangleMesh.create_coordinate_frame()
# スケーリング係数(各軸方向に対して)
scale =2.0 # 等方的スケーリング(各軸2.0倍)
# 回転行列(XYZオイラー角)
rotation = mesh.get_rotation_matrix_from_xyz((0, np.pi / 3, 0)) # Y60°
# 同次変換行列の初期化
T = np.eye(4)
# スケーリング+回転の合成(3×3の線形変換部分)
T[:3, :3] = scale * rotation
# 並進(x方向 +1.0, y方向 +2.0)
T[0, 3] = 1.0
T[1, 3] = 2.0
# -----------------------------
# 変換の適用と可視化
# -----------------------------
# mesh のコピーを作成し、同次変換を適用
mesh_t = copy.deepcopy(mesh).transform(T)
# 並べて表示(座標軸、原点にある元の座標フレーム,変換後の座標フレーム)
o3d.visualization.draw_geometries([axis, mesh, mesh_t])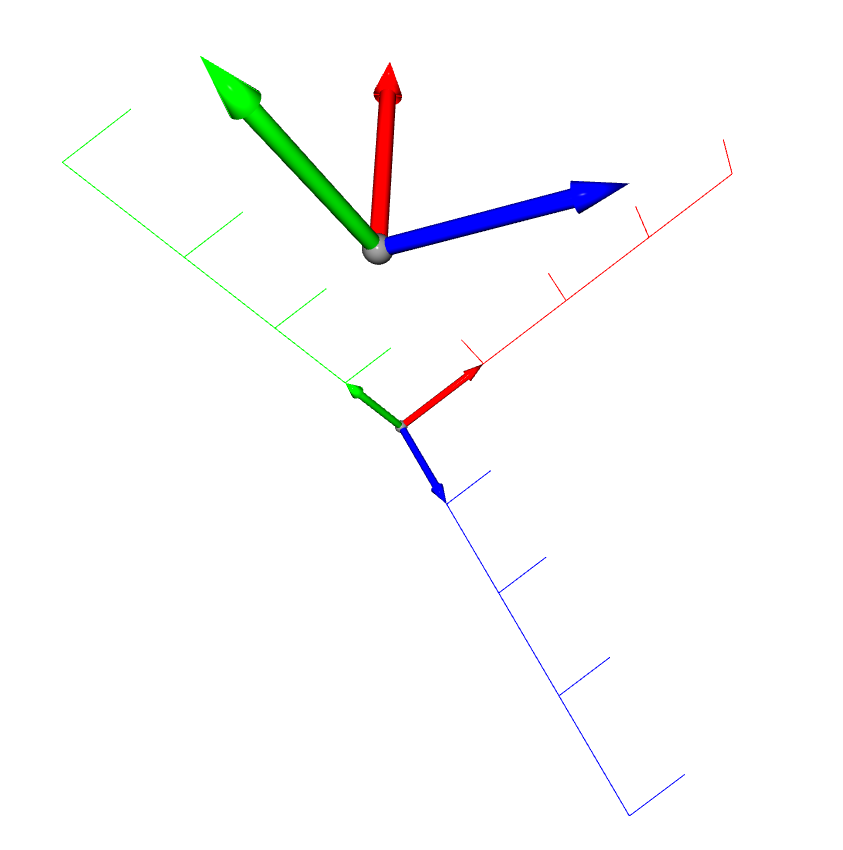
サンプルコード解説
- axis = my_function.create_axis(4, 1, 0.5)
全長4.0、目盛間隔1.0、目盛長0.5のカスタム座標軸を作成。自作モジュールを使用している。詳細はこちらの記事。 - mesh = o3d.geometry.TriangleMesh.create_coordinate_frame()
原点に単位長さの座標フレームを作成 - scale =2.0
各軸2.0倍にするためのスケールを定義 - rotation = mesh.get_rotation_matrix_from_xyz((0, np.pi / 3, 0))
Y軸中心に60度回転する回転行列(XYZオイラー角)を定義 - T = np.eye(4)
同次変換行列の初期化 - T[:3, :3] = scale * rotation
スケーリング+回転を合成し、同次変換行列に代入。 - T[0, 3] = 1.0
T[1, 3] = 2.0
並進(x方向 +1.0, y方向 +2.0)成分を同次変換行列に代入 - mesh_t = copy.deepcopy(mesh).transform(T)
mesh のコピーを作成し、同次変換を適用 - o3d.visualization.draw_geometries([axis, mesh, mesh_t])
並べて表示
まとめ
本記事では、並進・回転・スケール変換について簡単な例をサンプルコードにて説明したのち、三つの変換を同時に実行可能な同次変換について説明しました。
個人的には、別記事で作成した座標軸があることで、より変換前後がわかりやすく表示できたことが良かったかなと思います。
三次元点群処理は二次元の画像処理よりも情報が少なく、手探りで書籍や論文、公式ドキュメントを調査する日々です。
その中で、導入しやすいPythonとOpen3Dで三次元点群処理を体系的にまとめた書籍が以下になります。現在数少ない三次元点群処理の書籍ですので私も重宝しています。是非参考にしてみてください。
参考
社内外で評価されるエンジニアになる、ひいてはエンジニア人生を楽しくするためには、
日常のインプットとアウトプットの重要性が日に日に増していることを実感しています。
そのなかで、私は「書籍による学習」と「ブログによるアウトプット」を強くおすすめしております。
その重要性や効果の実感をブログに書いてみましたので、参考にしていただければ幸いです。